EQUAÇÃO GERAL DE GRACELI.

 G ψ = E ψ =  E [G+].... ..  =

G ψ = E ψ =  E [G+ψ ω /c] =   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

SISTEMA GRACELI DE:

 TENSOR G+ GRACELI = SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA., POTENCIAL DE ENERGIA, POTENCIAL QUÍMICO,  SISTEMA GRACELI DO INFINITO DIMENSIONAL.

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Na física, a mecânica quântica relativista (RQM) é qualquer formulação covariante de Poincaré de mecânica quântica. Esta teoria é aplicável a partículas massivas^[1] que se propagam em todas as velocidades até as comparáveis à velocidade da luz c e podem acomodar partículas sem massa.^[2][3] A teoria tem aplicação em física de alta energia,^[4] física de partículas e física de aceleradores,^[5][6] bem como física atômica, química^[7] e física da matéria condensada.^[8][9]

Operador de velocidade

O operador de velocidade Schrödinger/Pauli pode ser definido para uma partícula maciça usando a definição clássica p = m v, e substituindo os operadores quânticos da maneira usual:^[10]

${\displaystyle {\hat {\mathbf {v} }}={\frac {1}{m}}{\hat {\mathbf {p} }}}$ 

 /  G ψ = E ψ =  E [G+].... .. 

que possui autovalores que possuem qualquer valor. Na RQM, a teoria de Dirac, é:

${\displaystyle {\hat {\mathbf {v} }}={\frac {i}{\hbar }}\left[{\hat {H}},{\hat {\mathbf {r} }}\right]}$ /

 /  G ψ = E ψ =  E [G+].... ..

que deve ter autovalores entre ± c. Mais antecedentes teóricos podem ser visto na transformação de Foldy-Wouthuysen.^{[11][12][13][14]}

Equação de Klein-Gordon

Como foi dito acima, quando Schrödinger primeiro procurou uma equação que regesse os sistemas quânticos, pautou sua busca admitindo uma aproximação relativista, encontrando a depois redescoberta equação de Klein-Gordon:

${\displaystyle \left[\square +\left({\frac {mc}{\hbar }}\right)^{2}\right]\psi =0}$  /  G ψ = E ψ =  E [G+].... ..

onde

${\displaystyle \square \equiv \eta _{\nu \mu }\partial _{\nu }\partial ^{\nu }}$  /  G ψ = E ψ =  E [G+].... ..

A equação de Klein-Gordon, às vezes chamada de equação de Klein-Fock-Gordon (ou ainda Klein-Gordon-Fock) pode ser deduzida de algumas maneiras diferentes.

Usando-se a definição relativística de energia

${\displaystyle E^{2}=\left.p^{2}c^{2}+m^{2}c^{4}\right.}$  /  G ψ = E ψ =  E [G+].... ..

chega-se à equação:

${\displaystyle {\sqrt {(-i\mathbf {\nabla } )^{2}+m^{2}}}\psi =i{\frac {\partial }{\partial t}}\psi }$  /  G ψ = E ψ =  E [G+].... ..

Essa expressão, por conter operadores diferenciais sob o radical, além de apresentar dificuldades computacionais, também apresenta dificuldades conceituais, já que se torna uma teoria não-local (pelo fato de a raiz poder ser expressa como uma série infinita). Por ser uma equação de segunda ordem não permite que fique bem definida a questão da normalização da função de onda.

Fock deduziu-a através da generalização da equação de Schrödinger para campos magnéticos (onde as forças dependem da velocidade). Fock e Klein usaram ambos o método de Kaluza-Klein para deduzi-la. O motivo, só mais tarde entendido, da inadequação desta equação ao átomo de hidrogênio é que ela se aplica bem somente a partículas sem carga e de spin nulo.

Na mecânica quântica, o método variacional é uma ferramenta matemática utilizada para encontrar aproximações do valor próprio de mais baixa energia ou estado fundamental. Os fundamentos para este método vêm do princípio variacional.

Este método consiste em escolher uma função de onda tentativa que dependa de um ou mais parâmetros, e encontrar os valores destes parâmetros para cada valor esperado onde a energia seja a menor possível. A função de onda obtida pela substituição dos parâmetros pelos valores encontrados será uma aproximação do estado fundamental da função de onda, e o valor esperado de energia neste estado será um majorante para a energia deste estado fundamental.

Definição

Suponha um espaço de Hilbert e um operador autoadjunto sobre o hamiltoniano H. Ignore-se possíveis complicações de um espectro contínuo, suponha um espectro discreto de H e os espaços esperados correspondentes para cada valor esperado λ

${\displaystyle \sum _{\lambda _{1},\,\lambda _{2}\in \mathrm {Spec} (H)}\langle \psi _{\lambda _{1}}|\psi _{\lambda _{2}}\rangle =\delta _{\lambda _{1}\lambda _{2}}}$ 

 /  G ψ = E ψ =  E [G+].... ..

onde ${\displaystyle \delta _{i,j}}$ é o delta de Kronecker

${\displaystyle {\hat {H}}\left|\psi _{\lambda }\right\rangle =\lambda \left|\psi _{\lambda }\right\rangle }$. 

 /  G ψ = E ψ =  E [G+].... ..

Estados físicos são normalizados, ou seja suas normas são iguais a 1. Suponha agora que o espaço seja limitado por baixo e que seu maior limite inferior seja ${\displaystyle E_{0}}$. Suponha também que o estado correspondente a |ψ> seja conhecido. O valor esperado de H será então

${\displaystyle \left\langle \psi |H|\psi \right\rangle =\sum _{\lambda _{1},\lambda _{2}\in \mathrm {Spec} (H)}\left\langle \psi |\psi _{\lambda _{1}}\right\rangle \left\langle \psi _{\lambda _{1}}|H|\psi _{\lambda _{2}}\right\rangle \left\langle \psi _{\lambda _{2}}|\psi \right\rangle }$  /  G ψ = E ψ =  E [G+].... ..

${\displaystyle =\sum _{\lambda \in \mathrm {Spec} (H)}\lambda \left|\left\langle \psi _{\lambda }|\psi \right\rangle \right|^{2}\geq \sum _{\lambda \in \mathrm {Spec} (H)}E_{0}\left|\left\langle \psi _{\lambda }|\psi \right\rangle \right|^{2}=E_{0}}$ 

 /  G ψ = E ψ =  E [G+].... ..V

Se variarmos para todos os possíveis estados com norma 1 para que se minimize o valor esperado de H, o menor valor seria ${\displaystyle E_{0}}$ e o estado correspondente seria um estado esperado de ${\displaystyle E_{0}}$. Quando varia-se sobre todo o espaço de Hilbert normalmente se obtém cálculos complexos demais e um subespaço necessita ser escolhido. A escolha de diferentes subespaços levam a diferentes aproximações e o processo de escolha do subespaço com melhor aproximação é chamado de ansatz.

Suponha que haja alguma sobreposição entre o ansatz e o estado fundamental (caso contrário seria um ansatz ruim). Então para se normalizar o subespaço do ansatz

${\displaystyle \left\langle \psi (\alpha _{i})|\psi (\alpha _{i})\right\rangle =1}$

e agora minimizando

${\displaystyle \varepsilon (\alpha _{i})=\left\langle \psi (\alpha _{i})|H|\psi (\alpha _{i})\right\rangle }$. 

 /  G ψ = E ψ =  E [G+].... ..

A teoria orbital de Rutherford encontrou uma dificuldade teórica resolvida por Niels Bohr.

• No momento em que temos uma carga elétrica negativa composta pelos elétrons girando ao redor de um núcleo de carga positiva, este movimento gera uma perda de energia devido a emissão de radiação constante. Num dado momento, os elétrons vão se aproximar do núcleo num movimento em espiral e cair sobre si.

Em 1911, Niels Bohr publicou uma tese que demonstrava o comportamento eletrônico dos metais. Na mesma época, foi trabalhar com Ernest Rutherford em Manchester, Inglaterra. Lá obteve os dados precisos do modelo atômico, que iriam lhe ajudar posteriormente.

Em 1913, observando as dificuldades do modelo de Rutherford, Bohr intensificou suas pesquisas visando uma solução teórica.

Em 1916, Niels Bohr retornou para Copenhague para atuar como professor de física. Continuando suas pesquisas sobre o modelo atômico de Rutherford.

Em 1920, nomeado diretor do Instituto de Física Teórica, Bohr acabou desenvolvendo um modelo atômico que unificava a teoria atômica de Rutherford e a teoria da mecânica quântica de Max Planck.

Sua teoria consistia que ao girar em torno de um núcleo central, os elétrons deveriam girar em órbitas específicas com níveis energizados. Realizando estudos nos elementos químicos com mais de dois elétrons, concluiu que se tratava de uma organização bem definida em orbitais. Descobriu ainda que as propriedades químicas dos elementos eram determinadas pelo orbital mais externo. Louis Victor Pierre Raymondi (sétimo duque de Broglie), onde todo corpúsculo atômico pode comportar-se de duas formas, como onda e como partícula.

Bohr propôs os seguintes postulados:

1. Um electrão num átomo move-se numa órbita circular em torno do núcleo sob a influência da força de Coulomb entre o electrão e o núcleo.

2. Um electrão move-se em uma órbita para a qual o seu momento angular orbital, ${\displaystyle {\vec {L}}}$ , é um múltiplo inteiro de ${\displaystyle \hbar }$.

3. Um electrão, movendo-se numa órbita permitida, não irradia energia electromagnética. Assim, sua energia total E permanece constante.

4. Radiação electromagnética é emitida se um electrão, inicialmente movendo-se em uma órbita de energia total ${\displaystyle E_{i}}$ descontinuamente altera o seu movimento para que ele se possa mover em uma órbita de energia total ${\displaystyle E_{f}}$.

A frequência da radiação emitida v é igual à quantidade

${\displaystyle {\frac {(E_{i}-E_{f})}{h}}}$  /  G ψ = E ψ =  E [G+].... ..

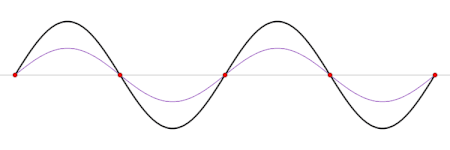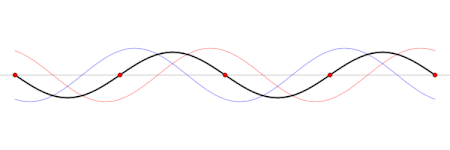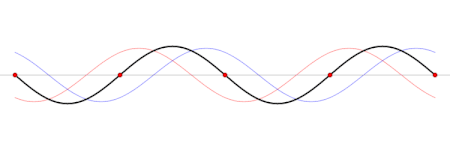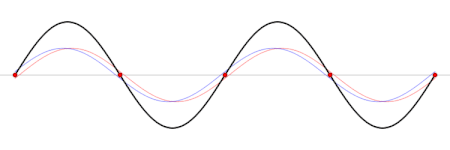
Ondas estacionárias

Uma onda estacionária é uma forma contínua de modo normal. Numa onda estacionária, todos os elementos do espaço (ou seja as coordenadas (x,y,z)) oscilam com a mesma frequência e em fase (alcançando o ponto de equilíbrio juntas), mas cada uma delas com uma amplitude diferente.

A forma general de uma onda estacionária é:

${\displaystyle \Psi (t)=f(x,y,z)(A\cos(\omega t)+B\sin(\omega t))}$ 

 /  G ψ = E ψ =  E [G+].... ..

onde f(x, y, z) representam a dependência da amplitude com a posição e o seno e coseno são as oscilações no decurso do tempo.

Onda estacionária gerada pela sobreposição de duas ondas viajantes. Observa-se a onda estacionária de cor negra, a onda de cor celeste desloca-se até à direita, enquanto que a onda de cor vermelha desloca-se até à esquerda. Em cada ponto e instante de tempo a onda negra obtem-se somando os valores de deslocamento nessa posição e esse instante de tempo.

Em termos físicos, as ondas estacionárias são produzidas pela interferência (sobreposição) de ondas e suas reflexões (apesar de que também é possível dizer justamente o oposto; que uma onda viajante é uma sobreposição de ondas estacionárias). A forma geométrica do meio determina qual será o padrão de interferência, ou seja determina a forma f(x, y, z) da onda estacionária. Esta dependência no espaço é chamada um modo normal.

Usualmente, em problemas com dependência contínua de (x,y,z) não existe um número determinado de modos normais, em mudança existe um número infinito de modos normais. Se o problema está delimitado (ou seja está definido numa porção restringida do espaço) existe um número discreto infinito de modos normais (usualmente numerados n = 1,2,3,...). Se o problema não está delimitado, existe um espectro contínuo de modos normais.

As frequências permitidas dependem dos modos normais como também das constantes físicas do problema (densidade, tensão, pressão, etc.) o que determina a velocidade de fase da onda. A classe de todas as frequências normais é no geral chamado o espectro de frequências. De modo geral, cada frequência está modulada pela amplitude na qual foi gerado, dando lugar a um gráfico do espectro de potência das oscilações.

No âmbito da música, os modos normais de vibração dos instrumentos (cordas, sopro, percussão, etc.) são chamados "harmónicos".

Modos normais em mecânica quântica

Em mecânica quântica, o estado ${\displaystyle \ |\psi \rangle }$ de um sistema descreve-se pela sua função de onda ${\displaystyle \ \psi (x,t)}$, a qual é uma solução da equação de Schrödinger. O quadrado do valor absoluto de ${\displaystyle \ \psi }$ , ou seja:

${\displaystyle \ P(x,t)=|\psi (x,t)|^{2}}$ 

 /  G ψ = E ψ =  E [G+].... ..

é a densidade de probabilidade de medir a partícula na posição x no tempo t.

Usualmente, quando se relaciona com algum tipo de potencial, a função de onda descompõe-se na sobreposição de autovectores de energia definida, cada um oscilando com uma frequência ${\displaystyle \omega =E_{n}/\hbar }$. Portanto, pode-se expressar:

${\displaystyle |\psi (t)\rangle =\sum _{n}|n\rangle \left\langle n|\psi (t=0)\right\rangle e^{-iE_{n}t/\hbar }}$ 

 /  G ψ = E ψ =  E [G+].... ..

Os autovectores possuem um significado físico mais além da base ortonormal. Quando se mede a energia do sistema, a função de onda colapsa num de seus autovectores e portanto a função de onda da partícula descreve-se pelo autovector puro correspondente à energea medida.

Spin de partículas elementares

Partículas elementares, tais como os fótons, elétrons e os quarks, são partículas que não podem ser divididas em partes menores. Teorias e estudos experimentais têm mostrado que o spin, presente nessas partículas, não pode ser explicado por postulações clássicas, onde partículas menores tendem a orbitar em volta de um centro de massa. O spin que essas partículas apresentam é uma propriedade física intrínseca, como a propriedade de carga elétrica e massa. Na mecânica quântica, o momento angular de qualquer sistema é expresso pela equação abaixo:

${\displaystyle S=\hbar {\sqrt {s(s+1)}}}$  /  G ψ = E ψ =  E [G+].... ..

Onde ${\displaystyle \hbar }$ é a constante de Planck reduzida ${\displaystyle {\frac {h}{2\pi }}}$,  /  G ψ = E ψ =  E [G+].... ..

e o número quântico do spin s é uma fração na forma ${\displaystyle s={\frac {n}{2}}}$ , onde n pode ser qualquer número inteiro não-negativo. Assim, s pode assumir os valores 0, ${\textstyle {\ce {{\frac {1}{2}}}}}$, 1, ${\textstyle {\frac {3}{2}}}$, 2, etc. A fração do número quântico é a maior diferença entre o momento angular orbital do spin. O valor de s depende unicamente do tipo de partícula, não podendo ser alterada de forma alguma, ao contrário da direção do spin.